La dinámica es una rama fundamental de la mecánica que estudia el movimiento de los cuerpos y las fuerzas que lo producen. En el análisis de problemas de ingeniería, la dinámica se divide en dos grandes áreas: la cinemática y la cinética.
La cinemática se enfoca en describir el movimiento sin considerar las causas que lo generan. Analiza trayectorias, velocidades y aceleraciones utilizando herramientas matemáticas y vectoriales que permiten modelar el comportamiento de cuerpos en movimiento, ya sea en línea recta o en rotación.
Por otro lado, la cinética estudia la relación entre el movimiento y las fuerzas que lo originan. Aplica las leyes de Newton y principios como la conservación del momento lineal y angular para entender cómo las fuerzas afectan el comportamiento dinámico de los sistemas.
Índice
- Movimiento Rectilíneo de Partículas: Posición, Velocidad y Aceleración.
- Formulas Clave del Movimiento de Partículas: Lo Que Todo Ingeniero Debe Conocer
- Cómo Analizar el Movimiento de una Partícula Paso a Paso
- Movimiento Rectilíneo: Entiende el MRU, MRUA y el Movimiento Relativo de Partículas
- Procedimiento para la Resolución de Problemas de MRU y MRUA
- A. Movimiento independiente de partículas
- B. Movimiento dependiente de partículas
- Ejercicio 11.33Ejercicio 11.34Ejercicio 11.35Ejercicio 11.36Ejercicio 11.37Ejercicio 11.38Ejercicio 11.39 Una automovilista entra a una carretera a 45 Kkm/h y acelera uniformemente hasta 99 km/h. De acuerdo con el odómetro del automóvil, la conductora sabe que recorrió 0.2 km mientras acelera. Detreminar a) la aceleración del automóvil, b)el tiempo que se requiere para alcanzar 99 km/h. Un camión recorre 220 m en 10 s mientras se desacelera a una razón constante de 0.6 m/s². Determine a) su velocidad inicial, b) su velocidad final, c) la distancia recorrida durante los primeros 1.5 s. Si se supone de una aceleración uniforme 11 ft/s² y se sabe que la rapídez de un automóvil cuando pasa por A es de 30 mi/h, determine a) el tiempo requerido para que el automóvil llegue a B, b) la rapídez del automóvil cuando pasa por B. Un grupo de estudiantes lanza un cohete a escala en dirección vertical. Con base en los datos registrados, determinan que la altitud del cohete fue de 89.6 ft en la parte final del vuelo en la que el cohete aún tenía impulso, y que el cohete aterriza 16 s después. Si se sabe que el paracaídas de descenso no pudo abrir y que el cohete descendió en caída libre hasta el suelo después de alcanzar la altura máxima, y suponiendo que g 32.2 ft/s², determine a) la rapidez v₁ del cohete al final del vuelo con impulso, b) la altura máxima alcanzada por el cohete.
- Un atleta en una carrera de 100 m acelera de manera uniforme durante los primeros 35 m y luego corre con una velocidad constante. Si el tiempo del atleta para los primeros 35 mes de 5.4 s, determine a) su aceleración, b) su velocidad final y c) el tiempo en que completa la carrera. Un paquete pequeño se suelta desde el reposo en A y se mueve a lo largo del transportador ABCD formando por ruedas deslizantes. El paquete tiene una aceleración uniforme de 4.8 m/s² mientras desciende sobre las secciones AB Y CD, y su velocidad es constante entre B y C. Si la velocidad del paquete en D es de 7.2 m/s, determine a) la distancia d entre C y D, b) el tiempo requerido para que el paquete llegue a D. Un oficial de policía en una patrulla estacionada en una zona donde la rapidez es de 70 km/h observa el paso de un automóvil que marcha a una rapidez constante. Al oficial le parece que el conductor podría estar intoxicado y arranca la patrulla, acelera uniformemente hasta 90 km/hr en 8 s y mantiene una velocidad constante de 90 km/h, alcanza al automovilista 42 s después. Si se sabe que transcurrieron 18 s antes de que el ofical empezara a perseguir al automovilista, determine a) la distancia que recorrió el oficial antes de alcanzar al automovilista, b) la rapidez del automovilista.
Movimiento Rectilíneo de Partículas: Posición, Velocidad y Aceleración.
El movimiento rectilíneo es un tipo de movimiento en el que una partícula se desplaza a lo largo de una línea recta. Para analizarlo, se utilizan tres magnitudes fundamentales: posición, velocidad y aceleración, todas tratadas como vectores en dinámica.
- Posición (𝑟): Es la ubicación de la partícula en el espacio respecto a un punto de referencia. En el movimiento rectilíneo, puede representarse como una función escalar del tiempo, x(t), sobre un eje definido.
- Velocidad (𝑣): Es la tasa de cambio de la posición respecto al tiempo. Se expresa como la derivada de la posición:v(t)=dx(t)/dt La velocidad puede ser constante o variable, positiva (movimiento hacia adelante) o negativa (movimiento hacia atrás).
- Aceleración (𝑎): Es la tasa de cambio de la velocidad respecto al tiempo. Se obtiene como la derivada de la velocidad:a(t)=dv(t)/dt=d^2x(t)/dt^2.Indica si la partícula está acelerando o desacelerando, y su signo depende del sentido del cambio en la velocidad.
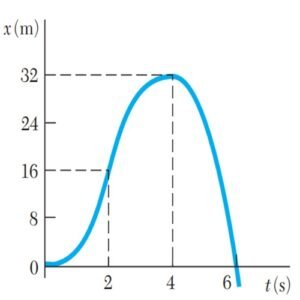
Formulas Clave del Movimiento de Partículas: Lo Que Todo Ingeniero Debe Conocer
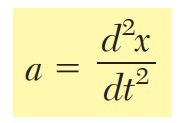
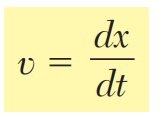
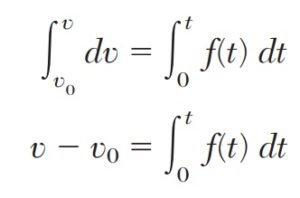
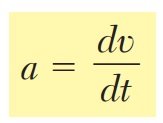
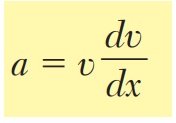
![]()
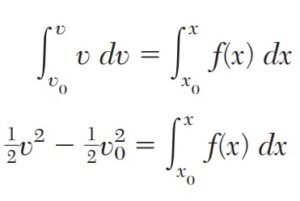
Cómo Analizar el Movimiento de una Partícula Paso a Paso
En los problemas de esta lección se busca determinar la posición, velocidad o aceleración de una partícula en movimiento rectilíneo, es fundamental identificar la variable independiente (generalmente t o x) y lo que se debe encontrar (por ejemplo, v en función de x), se recomienda iniciar cada ejercicio escribiendo los datos dados y el objetivo del problema.
Se consideran cuatro casos principales:
- Dada x(t): obtener v(t)v(t) y a(t)a(t)
- Se derivan x(t) una y dos veces para obtener la velocidad y aceleración.
- Si velocidad y aceleración tienen signos opuestos, puede haber cambio de dirección.
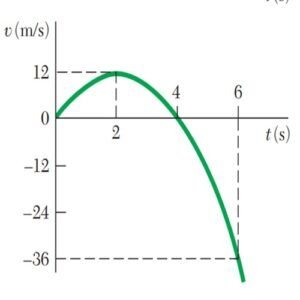
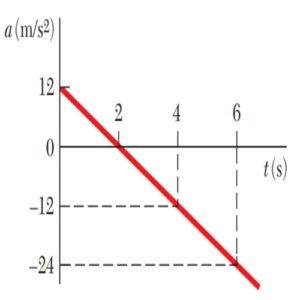
- Es útil construir un diagrama de movimiento con eventos clave (como cuando v=vmax y v= 0) para visualizar el comportamiento.
- Dada a(t): obtener v(t) y x(t)
- Se integran a(t) usando condiciones iniciales (como t=0, v=vinicial).
- Si a(t) incluye constantes desconocidas, se determinan usando valores conocidos.
- Dada a(x): obtener v(x) y x(t)
- Se integran usando estados conocidos (por ejemplo, x=x1, v=v1).
- Como a=0 cuando v es máxima, se halla el punto de velocidad máxima resolviendo a(x)=0.
- Dada a(v): obtener v(x), v(t) y x(t)
- Se aplican técnicas similares a los casos anteriores.
- Se utilizan las relaciones fundamentales:v=dx/dt, a=dv/dt, a=v dv/dx
Movimiento Rectilíneo: Entiende el MRU, MRUA y el Movimiento Relativo de Partículas
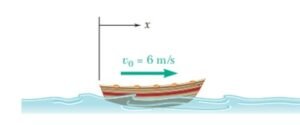
El estudio del movimiento rectilíneo es fundamental en la física, ya que permite comprender cómo se desplazan los objetos en línea recta bajo diferentes condiciones, dentro de este tipo de movimiento, destacan dos casos esenciales: el Movimiento Rectilíneo Uniforme (MRU), en el que un cuerpo se desplaza con velocidad constante, y el Movimiento Rectilíneo Uniformemente Acelerado (MRUA), donde la aceleración es constante y la velocidad varía de forma uniforme. Ambos modelos son la base para analizar fenómenos cotidianos como un automóvil que mantiene su velocidad o uno que acelera progresivamente.
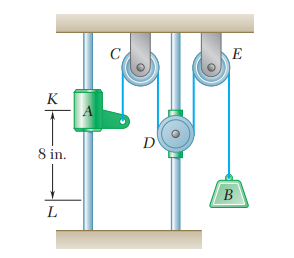
Además, en muchos contextos prácticos es necesario estudiar el movimiento de varias partículas al mismo tiempo, esto incluye el movimiento relativo entre dos partículas, que permite entender cómo se mueve una con respecto a la otra, y los movimientos dependientes, donde el desplazamiento de una partícula está ligado al de otra, como ocurre con sistemas de poleas o mecanismos conectados.
Comprender estos conceptos es clave para resolver problemas de cinemática, diseñar sistemas mecánicos y predecir el comportamiento de objetos en movimiento,en esta guía exploraremos cada uno de estos tipos de movimiento con ejemplos y explicaciones claras.
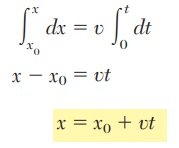
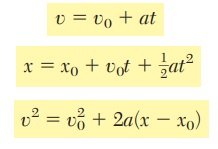
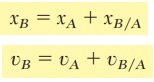
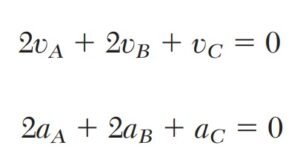
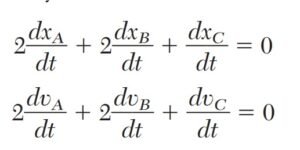
![]()
Procedimiento para la Resolución de Problemas de MRU y MRUA
A. Movimiento independiente de partículas
Para resolver problemas en los que las partículas se mueven de manera independiente, se sugiere seguir estos pasos:
- Preparación: Comienza listando los datos, haciendo un dibujo del sistema y eligiendo un origen y una dirección positiva para el eje de coordenadas.
- Ecuaciones: Escribe las ecuaciones que describen el movimiento de cada partícula y sus relaciones mutuas.
- Condiciones iniciales: Define el estado del sistema en el tiempo inicial (). Si las partículas no comienzan a moverse simultáneamente, se pueden usar dos enfoques:
- Establecer cuando las partículas inician su movimiento, ajustando las posiciones y velocidades iniciales según corresponda.
- Establecer con el inicio de la primera partícula, y en las ecuaciones de las demás, sustituir por (donde es su tiempo de inicio).
B. Movimiento dependiente de partículas
Este método se aplica a problemas donde las partículas están físicamente conectadas, generalmente por cables o cuerdas, el proceso es similar al anterior, pero con un enfoque en las restricciones de movimiento:
- Bosquejo y coordenadas: Realiza un bosquejo y selecciona un sistema de coordenadas con un sentido positivo claro para cada eje.
- Ecuación de ligadura: Escribe una ecuación que describa la restricción impuesta por cada conexión (cable), al diferenciar esta ecuación dos veces, se obtienen las relaciones entre las velocidades y aceleraciones de las partículas.
- Coordenadas simples: Si hay múltiples direcciones de movimiento, define un eje para cada una y ubica los orígenes de manera que las ecuaciones de restricción sean lo más sencillas posible.
Ejercicio 11.33Ejercicio 11.34Ejercicio 11.35Ejercicio 11.36Ejercicio 11.37Ejercicio 11.38Ejercicio 11.39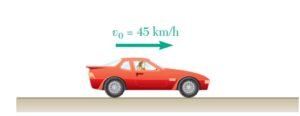 Una automovilista entra a una carretera a 45 Kkm/h y acelera uniformemente hasta 99 km/h. De acuerdo con el odómetro del automóvil, la conductora sabe que recorrió 0.2 km mientras acelera. Detreminar a) la aceleración del automóvil, b)el tiempo que se requiere para alcanzar 99 km/h.
Una automovilista entra a una carretera a 45 Kkm/h y acelera uniformemente hasta 99 km/h. De acuerdo con el odómetro del automóvil, la conductora sabe que recorrió 0.2 km mientras acelera. Detreminar a) la aceleración del automóvil, b)el tiempo que se requiere para alcanzar 99 km/h.
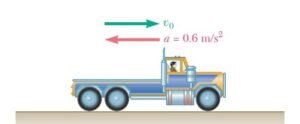 Un camión recorre 220 m en 10 s mientras se desacelera a una razón constante de 0.6 m/s². Determine a) su velocidad inicial, b) su velocidad final, c) la distancia recorrida durante los primeros 1.5 s.
Un camión recorre 220 m en 10 s mientras se desacelera a una razón constante de 0.6 m/s². Determine a) su velocidad inicial, b) su velocidad final, c) la distancia recorrida durante los primeros 1.5 s. 
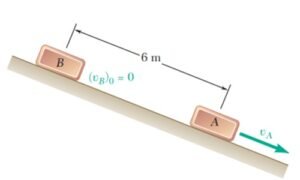
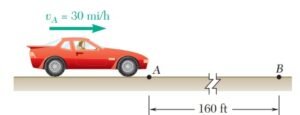 Si se supone de una aceleración uniforme 11 ft/s² y se sabe que la rapídez de un automóvil cuando pasa por A es de 30 mi/h, determine a) el tiempo requerido para que el automóvil llegue a B, b) la rapídez del automóvil cuando pasa por B.
Si se supone de una aceleración uniforme 11 ft/s² y se sabe que la rapídez de un automóvil cuando pasa por A es de 30 mi/h, determine a) el tiempo requerido para que el automóvil llegue a B, b) la rapídez del automóvil cuando pasa por B. 
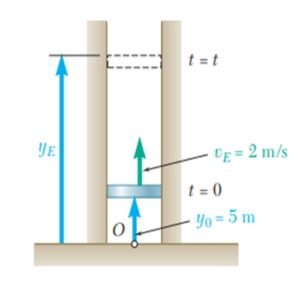
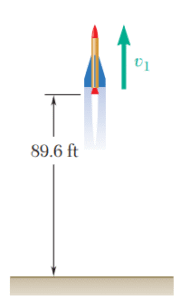 Un grupo de estudiantes lanza un cohete a escala en dirección vertical. Con base en los datos registrados, determinan que la altitud del cohete fue de 89.6 ft en la parte final del vuelo en la que el cohete aún tenía impulso, y que el cohete aterriza 16 s después. Si se sabe que el paracaídas de descenso no pudo abrir y que el cohete descendió en caída libre hasta el suelo después de alcanzar la altura máxima, y suponiendo que g 32.2 ft/s², determine a) la rapidez v₁ del cohete al final del vuelo con impulso, b) la altura máxima alcanzada por el cohete.
Un grupo de estudiantes lanza un cohete a escala en dirección vertical. Con base en los datos registrados, determinan que la altitud del cohete fue de 89.6 ft en la parte final del vuelo en la que el cohete aún tenía impulso, y que el cohete aterriza 16 s después. Si se sabe que el paracaídas de descenso no pudo abrir y que el cohete descendió en caída libre hasta el suelo después de alcanzar la altura máxima, y suponiendo que g 32.2 ft/s², determine a) la rapidez v₁ del cohete al final del vuelo con impulso, b) la altura máxima alcanzada por el cohete. 
 Un atleta en una carrera de 100 m acelera de manera uniforme durante los primeros 35 m y luego corre con una velocidad constante. Si el tiempo del atleta para los primeros 35 mes de 5.4 s, determine a) su aceleración, b) su velocidad final y c) el tiempo en que completa la carrera.
Un atleta en una carrera de 100 m acelera de manera uniforme durante los primeros 35 m y luego corre con una velocidad constante. Si el tiempo del atleta para los primeros 35 mes de 5.4 s, determine a) su aceleración, b) su velocidad final y c) el tiempo en que completa la carrera.
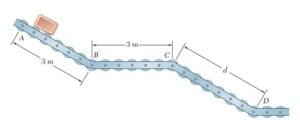 Un paquete pequeño se suelta desde el reposo en A y se mueve a lo largo del transportador ABCD formando por ruedas deslizantes. El paquete tiene una aceleración uniforme de 4.8 m/s² mientras desciende sobre las secciones AB Y CD, y su velocidad es constante entre B y C. Si la velocidad del paquete en D es de 7.2 m/s, determine a) la distancia d entre C y D, b) el tiempo requerido para que el paquete llegue a D.
Un oficial de policía en una patrulla estacionada en una zona donde la rapidez es de 70 km/h observa el paso de un automóvil que marcha a una rapidez constante. Al oficial le parece que el conductor podría estar intoxicado y arranca la patrulla, acelera uniformemente hasta 90 km/hr en 8 s y mantiene una velocidad constante de 90 km/h, alcanza al automovilista 42 s después. Si se sabe que transcurrieron 18 s antes de que el ofical empezara a perseguir al automovilista, determine a) la distancia que recorrió el oficial antes de alcanzar al automovilista, b) la rapidez del automovilista.
Un paquete pequeño se suelta desde el reposo en A y se mueve a lo largo del transportador ABCD formando por ruedas deslizantes. El paquete tiene una aceleración uniforme de 4.8 m/s² mientras desciende sobre las secciones AB Y CD, y su velocidad es constante entre B y C. Si la velocidad del paquete en D es de 7.2 m/s, determine a) la distancia d entre C y D, b) el tiempo requerido para que el paquete llegue a D.
Un oficial de policía en una patrulla estacionada en una zona donde la rapidez es de 70 km/h observa el paso de un automóvil que marcha a una rapidez constante. Al oficial le parece que el conductor podría estar intoxicado y arranca la patrulla, acelera uniformemente hasta 90 km/hr en 8 s y mantiene una velocidad constante de 90 km/h, alcanza al automovilista 42 s después. Si se sabe que transcurrieron 18 s antes de que el ofical empezara a perseguir al automovilista, determine a) la distancia que recorrió el oficial antes de alcanzar al automovilista, b) la rapidez del automovilista.
 Una automovilista entra a una carretera a 45 Kkm/h y acelera uniformemente hasta 99 km/h. De acuerdo con el odómetro del automóvil, la conductora sabe que recorrió 0.2 km mientras acelera. Detreminar a) la aceleración del automóvil, b)el tiempo que se requiere para alcanzar 99 km/h.
Una automovilista entra a una carretera a 45 Kkm/h y acelera uniformemente hasta 99 km/h. De acuerdo con el odómetro del automóvil, la conductora sabe que recorrió 0.2 km mientras acelera. Detreminar a) la aceleración del automóvil, b)el tiempo que se requiere para alcanzar 99 km/h. Un camión recorre 220 m en 10 s mientras se desacelera a una razón constante de 0.6 m/s². Determine a) su velocidad inicial, b) su velocidad final, c) la distancia recorrida durante los primeros 1.5 s.
Un camión recorre 220 m en 10 s mientras se desacelera a una razón constante de 0.6 m/s². Determine a) su velocidad inicial, b) su velocidad final, c) la distancia recorrida durante los primeros 1.5 s. 
 Si se supone de una aceleración uniforme 11 ft/s² y se sabe que la rapídez de un automóvil cuando pasa por A es de 30 mi/h, determine a) el tiempo requerido para que el automóvil llegue a B, b) la rapídez del automóvil cuando pasa por B.
Si se supone de una aceleración uniforme 11 ft/s² y se sabe que la rapídez de un automóvil cuando pasa por A es de 30 mi/h, determine a) el tiempo requerido para que el automóvil llegue a B, b) la rapídez del automóvil cuando pasa por B. 
 Un grupo de estudiantes lanza un cohete a escala en dirección vertical. Con base en los datos registrados, determinan que la altitud del cohete fue de 89.6 ft en la parte final del vuelo en la que el cohete aún tenía impulso, y que el cohete aterriza 16 s después. Si se sabe que el paracaídas de descenso no pudo abrir y que el cohete descendió en caída libre hasta el suelo después de alcanzar la altura máxima, y suponiendo que g 32.2 ft/s², determine a) la rapidez v₁ del cohete al final del vuelo con impulso, b) la altura máxima alcanzada por el cohete.
Un grupo de estudiantes lanza un cohete a escala en dirección vertical. Con base en los datos registrados, determinan que la altitud del cohete fue de 89.6 ft en la parte final del vuelo en la que el cohete aún tenía impulso, y que el cohete aterriza 16 s después. Si se sabe que el paracaídas de descenso no pudo abrir y que el cohete descendió en caída libre hasta el suelo después de alcanzar la altura máxima, y suponiendo que g 32.2 ft/s², determine a) la rapidez v₁ del cohete al final del vuelo con impulso, b) la altura máxima alcanzada por el cohete. 
 Un atleta en una carrera de 100 m acelera de manera uniforme durante los primeros 35 m y luego corre con una velocidad constante. Si el tiempo del atleta para los primeros 35 mes de 5.4 s, determine a) su aceleración, b) su velocidad final y c) el tiempo en que completa la carrera.
Un atleta en una carrera de 100 m acelera de manera uniforme durante los primeros 35 m y luego corre con una velocidad constante. Si el tiempo del atleta para los primeros 35 mes de 5.4 s, determine a) su aceleración, b) su velocidad final y c) el tiempo en que completa la carrera. Un paquete pequeño se suelta desde el reposo en A y se mueve a lo largo del transportador ABCD formando por ruedas deslizantes. El paquete tiene una aceleración uniforme de 4.8 m/s² mientras desciende sobre las secciones AB Y CD, y su velocidad es constante entre B y C. Si la velocidad del paquete en D es de 7.2 m/s, determine a) la distancia d entre C y D, b) el tiempo requerido para que el paquete llegue a D.
Un paquete pequeño se suelta desde el reposo en A y se mueve a lo largo del transportador ABCD formando por ruedas deslizantes. El paquete tiene una aceleración uniforme de 4.8 m/s² mientras desciende sobre las secciones AB Y CD, y su velocidad es constante entre B y C. Si la velocidad del paquete en D es de 7.2 m/s, determine a) la distancia d entre C y D, b) el tiempo requerido para que el paquete llegue a D.

