La cinemática angular es una rama esencial de la ingeniería que se enfoca en el estudio del movimiento de cuerpos rígidos, particularmente en lo que respecta a su rotación y desplazamiento angular, en este artículo, nos adentraremos en la cinemática de mecanismos, explicando cómo se pueden resolver problemas complejos que involucran movimientos tanto de translación como de rotación.
A lo largo del contenido, te proporcionaremos ejemplos de cinemática (Mecánica Vectorial para Ingenieros, Beer and Johnston) que te permitirán entender y aplicar conceptos clave como la velocidad angular, la aceleración angular y el desplazamiento angular, con esta guía, aprenderás a abordar de manera efectiva problemas típicos de la cinemática básica, lo que te ayudará a mejorar tus habilidades para analizar y diseñar mecanismos en ingeniería.
Índice
- Entendiendo los Movimientos de Rotación y Translación: Guía Completa para Resolución de Problemas de Cinemática
- Ejercicios de Cinemática Circular: Problemas Resueltos de Cinemática de Cuerpo Rígido.
- El movimiento de una leva se define por medio de la relación θ = t³ – 9t² + 15t, donde θ se expresa en radianes y t en segundos. Determine las coordenada angular, la velocidad angular y la aceleración angular de la leva cuando a) t = 0, b) t = 3 s.
- Para la leva del problema 15.1, determine el tiempo, la coordenada angular y la aceleración angular cuando la velocidad angular es cero.
- El movimiento de una manivela oscilante se define por medio de la relación θ = θ₀ Sen (πt/T) – (0.5θ₀) Sen (2πt/T), donde θ se expresa en radianes y t en segundos. Si se sabe que θ₀= 6 rad y T = 4s, determine la coordenada angular, la velocidad angular y la aceleración angular de la manivela cuando a) t = 0, b) t = 2s.
- Retome el problema 15.3, cuando t = 1s.
- El movimiento de un disco que gira en un baño de aceite se define mediante la relación θ = θ₀ [ 1- e^(-t/4)], donde θ se expresa en radianes y t en segundos. Si se sabe que θ₀=0.40 rad, determinar la coordenada angular, la velocidad angular y la aceleración angular del disco cuando a) t=0, b) t=3s, c) t=∞.
- La aceleración angular de un disco oscilante se define mediante la ecuación α=-kθ. Determine a) el valor de k para el cual w=8 rad/s cuando θ=0 y θ=4 rad cuando w=0, b) la velocidad angular del disco cuando θ=3rad.
- Cuando se pone en operación, un motor alcanza su velocidad nominal de 3,300 rpm en 6s y cuando el motor se desactiva tarda 80s para llegar al reposo. Si se supone que el movimiento es uniformemente acelerado, determinar el número de revoluciones que ejecuta el motor a) para alcanzar la velocidad nominal, b) para detenerse.
Entendiendo los Movimientos de Rotación y Translación: Guía Completa para Resolución de Problemas de Cinemática
Para poder resolver problemas de cinemática de cuerpo rigido es necesario comprender dos movimientos básicos, el de rotación y el de translación, a continuacion los definimos:
1. Movimiento de Translación: Es el movimiento en el que todos los puntos de un cuerpo rígido se mueven a la misma velocidad en una dirección específica, es decir, cada punto sigue una trayectoria paralela y no cambia la orientación del cuerpo, es el desplazamiento rectilíneo o curvilíneo de todo el cuerpo.
2. Movimiento de Rotación: Es el movimiento en el que un cuerpo rígido gira alrededor de un eje fijo, durante este movimiento, los puntos del cuerpo describen trayectorias circulares alrededor del eje, y la orientación del cuerpo cambia, pero su centro de masa permanece fijo.
Las fórmulas de cinemática permiten describir el movimiento de los cuerpos a partir de variables como posición, velocidad y aceleración. En el caso de los sólidos, las ecuaciones de cinemática para cuerpo rígido son esenciales para analizar tanto el movimiento de traslación como el de rotación, considerando que las distancias entre los puntos del cuerpo no cambian con el tiempo, acontinuación las formulas:
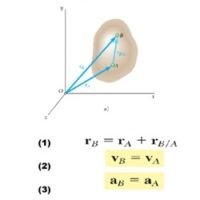
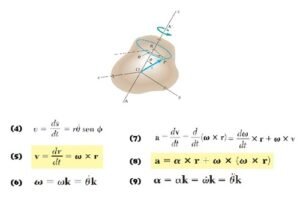
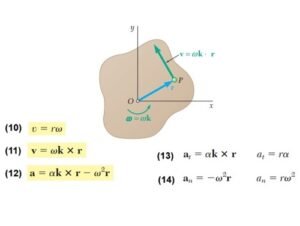
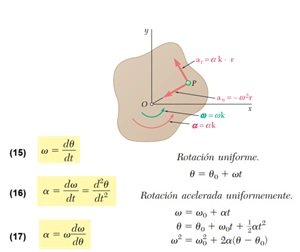
Ejercicios de Cinemática Circular: Problemas Resueltos de Cinemática de Cuerpo Rígido.
Recuerda que para poder entender la solución de los siguientes Ejercicios de Cinemática de Cuerpos Rigidos del Libro Mecánica Vectorial para Ingenieros, Beer-Jonhston-Cornwell, debes de contar con conocimientos en cálculo.
El movimiento de una leva se define por medio de la relación θ = t³ – 9t² + 15t, donde θ se expresa en radianes y t en segundos. Determine las coordenada angular, la velocidad angular y la aceleración angular de la leva cuando a) t = 0, b) t = 3 s.

Para la leva del problema 15.1, determine el tiempo, la coordenada angular y la aceleración angular cuando la velocidad angular es cero.

El movimiento de una manivela oscilante se define por medio de la relación θ = θ₀ Sen (πt/T) – (0.5θ₀) Sen (2πt/T), donde θ se expresa en radianes y t en segundos. Si se sabe que θ₀= 6 rad y T = 4s, determine la coordenada angular, la velocidad angular y la aceleración angular de la manivela cuando a) t = 0, b) t = 2s.

Retome el problema 15.3, cuando t = 1s.

El movimiento de un disco que gira en un baño de aceite se define mediante la relación θ = θ₀ [ 1- e^(-t/4)], donde θ se expresa en radianes y t en segundos. Si se sabe que θ₀=0.40 rad, determinar la coordenada angular, la velocidad angular y la aceleración angular del disco cuando a) t=0, b) t=3s, c) t=∞.


La aceleración angular de un disco oscilante se define mediante la ecuación α=-kθ. Determine a) el valor de k para el cual w=8 rad/s cuando θ=0 y θ=4 rad cuando w=0, b) la velocidad angular del disco cuando θ=3rad.

Cuando se pone en operación, un motor alcanza su velocidad nominal de 3,300 rpm en 6s y cuando el motor se desactiva tarda 80s para llegar al reposo. Si se supone que el movimiento es uniformemente acelerado, determinar el número de revoluciones que ejecuta el motor a) para alcanzar la velocidad nominal, b) para detenerse.


